2储罐的概述

大型储罐具有节省钢材、占地少、投资小及便于操作管理等优点。日本自20世纪60年代开始建造10万㎡以上的储罐，单罐最大容量177万m(不包括半地下式)[1]，目前国内也开始建造大型储罐。

   本文将利用大型分线性有限元程序ABAQUS对新设计的15万㎡大型储罐进行强度分析，以验证设计的储罐能否满足规范要求。

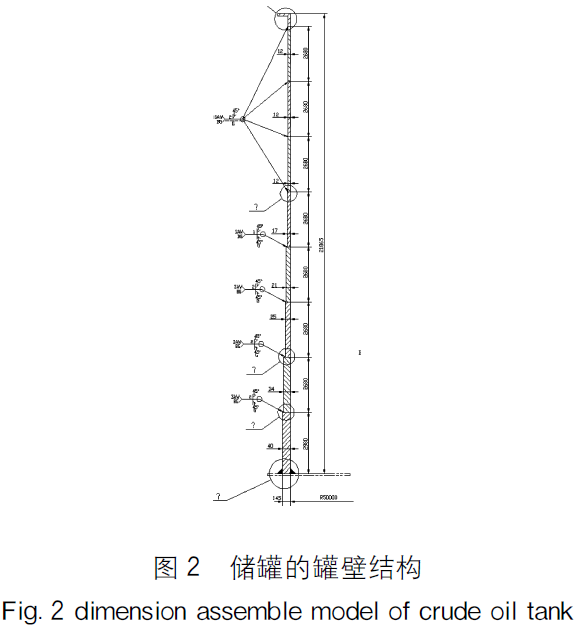
双盘式浮顶罐为圆筒形结构，结构总图见图1所示。储罐罐壁分为8段，见图2所示，储罐内径为c100m，高为21.865m。最上层管壁材料采用Q235-B，其余罐壁采用SPV490Q，该材料是日本牌号。底板由中幅板和边缘板组成，中幅板材料采用Q235-B边缘板材料采用SPV490Q。罐壁自上而下厚度依次为12mm、12mm、12mm、17mm、21mm、25mm、34mm、40mm，各段罐壁的高度除最下一段为298m外其余高度为268m。储罐基础为混凝土环梁+回填沙。

所使用的钢材和混凝土数材料力学性能参数如表1所示。钢材的强度和许用应力见表2所示。
表1常温下材料的力学性能参数
Table1Mechanicalparameter under room temperature

表2常温下钢材的强度和许用应力
Table 2 Strength and permissible stress of used steel under room temperature

根据美国石油协会标准APISTD590-1995水压试验时，材料的许用应力「o]一般取min(3/40s.31o)，其中0为材料的屈服强度，ob为材料的抗拉强度。由此确定的材料需用应力见表20

3储罐的有限元模型和分析结果
31有限元模型
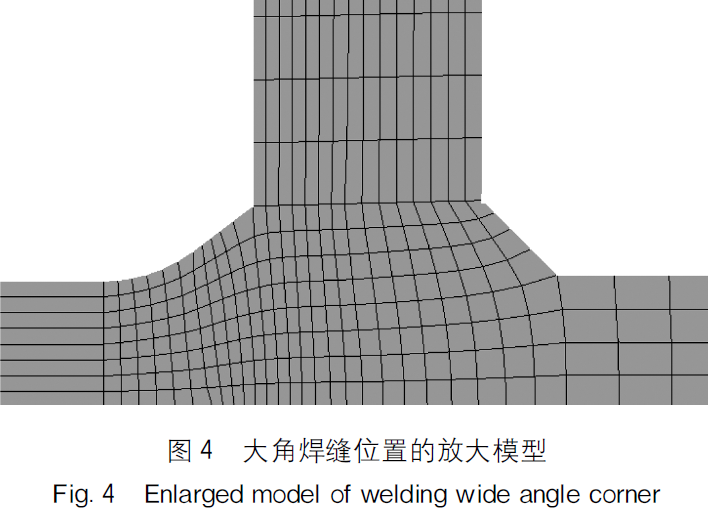
由于储罐结构是轴对称的，利用AUTOCAD平面图纸，直接在ABAQUS66软件内建立二维轴对称模型。模型中省略了饮水孔、盘梯等辅助设施，只建立罐侧壁和底面的模型。所建立的模型如图3所示，由于油罐的厚度相对于直径太小，在模型中没有显示出来。储罐共划分的单元类型为CAX4R，即4节点轴对称四边形单元，单元的全局大小为001。为保证在大角焊缝位置单元不会发生奇变，将图4中的导圆和导棱边都单独增加了节点数量。

图4是大角焊缝位置处的轴对称模型，外侧采用高13mm的导棱角，内侧与底板联接的部位采用半径26mm的导圆角，与侧板联接的部位采用53夹角的导棱角。

32边界条件
模型采用底部环板支撑的下边缘固定不动，为固支约束，中间地基的底部可以有轴向位移。计算时采用三种轴向位移进行比较0mm，10mm，20mm。根据法规规定计算，允许的地基沉降为350mm。但地基的沉降是同时进行的，不可能仅内部沉降，而四周的环板支撑完全不沉降。此处计算采用的沉降值是相对值。
罐底部与基础之间采用硬接触。
油罐地板受均匀压力217150Pa侧面受随高度变化的载荷，载荷的公式为，10000x(Y-21865)，其中Y为高度方向。考虑水压试验的情况，储液压力为p=ogh，水的密度为1000kg/m3，重力加速度g取10m/s。同时，储罐整体受向下的重力加速度g作用。

33计算结果
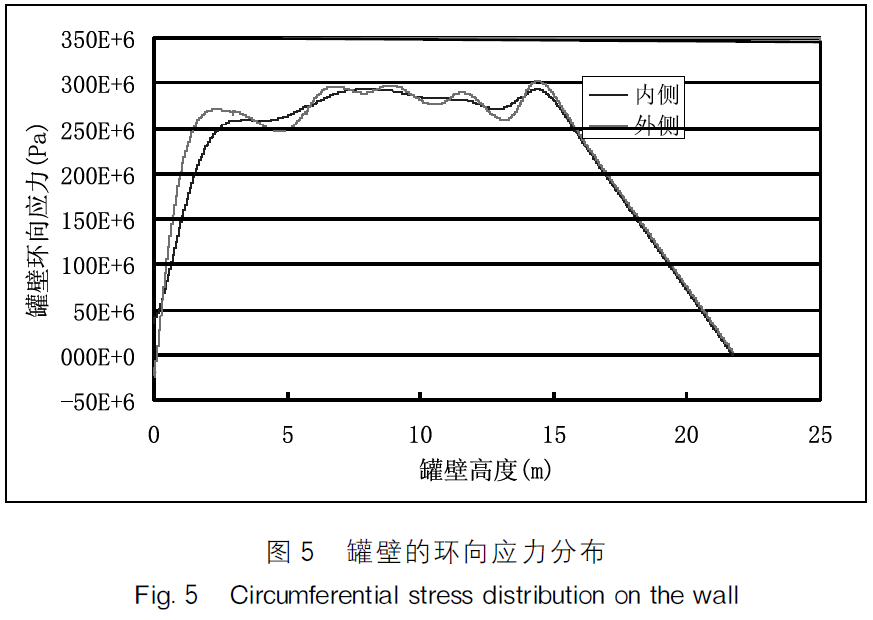
对整个模型进行弹性分析，得到整体结构的应力分布，先讨论储罐侧壁的应力计算结果。图5是储罐壁的环向应力分布，罐壁的内侧和外侧应力分布规 律基本相同。从图中可以看出，除最上和最下面的罐壁外，其它中间层的罐壁 环向应力基本保持在250~300MPa的范围内，说明设计符合等强度原理，即罐壁的应力水平应保持均匀并尽可能发挥 材料的强度。计算的最大环向应力值为 300MPa。从图中可以看出，最上和最下 罐壁高度(m) 层罐壁能够满足强度要求，最下层罐壁 图5罐壁的环向应力分布 的许用应力为261MPa，最上层罐壁的许 Fig5Circumferential stress distribution on the wall 用应力为161MPa。中间各层罐壁的环向应力大于许用应力值。

罐壁径向应力分布如图6所示。从图中可以看出，除最下一层罐壁内外侧有较大的压应力，其它各层罐壁轴向力为0。这是因为在罐的底部和罐最下层侧壁焊接在一起，存在一定弯矩作用，对罐壁产生压缩作用。对于其它各层罐壁，则由于不存在约束，基本无法产生径向力作用。

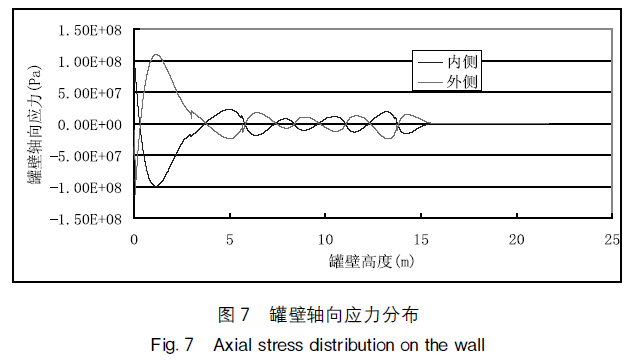
罐壁轴向应力分布如图7所示。从图中可以看出，除最下一层罐壁内侧有较大的拉应力，外侧有较大的压应力外，其它各层罐壁轴向力很小。这是因为在罐的底部由于弯矩的作用，对罐壁内侧产生拉伸作用，对罐壁外侧产生压缩作用，对于其它各层罐壁，则由干不存在约束，产生的轴向力很小。最大轴向力值为100MPao

罐底部的应力分布。罐底部由于回填材料的作用，应力水平比较低，除外部边缘焊缝处，其余部分的 Tresca应力在120MPa以下，径向应力在28Mpa以下，轴向应力在35Mpa以下，环向应力在90Mpa以下，因此罐底部强度有足够大的裕度。
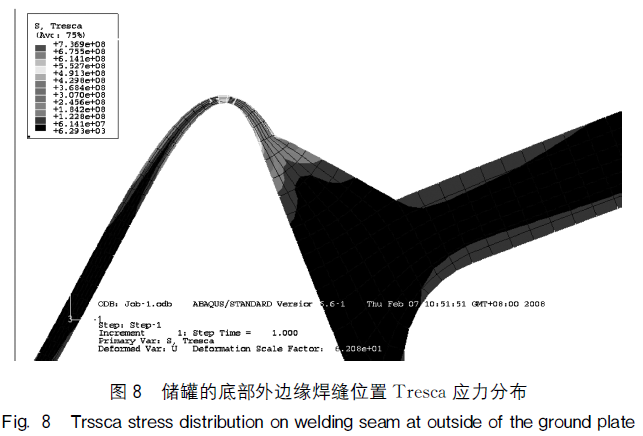
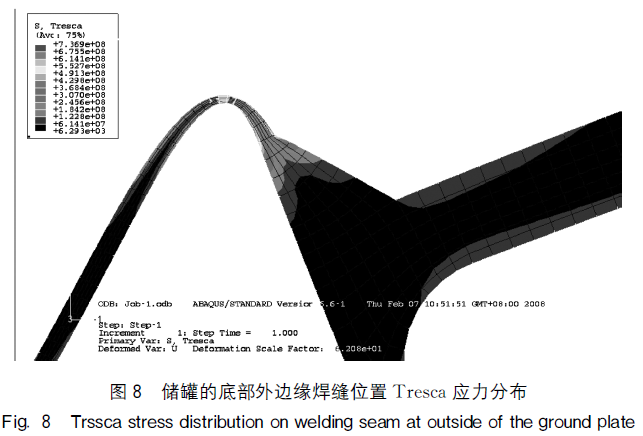
应力最大的部位是罐底部厚度最薄的部位与外侧底环板焊接的位置。由于罐底有1:100的倾角，从罐底中心部位逐渐减薄，到最外侧时厚度只有10mm，外侧底环板厚度为22mm，两个板的焊接部位最薄，计算表明，此处的应力最大，此处的Tresca应力分布如图8所示。由于罐壁和罐底结合处巨大的弯矩作用罐底部翘曲，从厚度最薄的部位附近翘起，产生很大的应力和应变，最大Tresca应力值为723MPa，环向应力最大值为218MPa，径向应力最大值为725MPa，轴向应力最大值为100MPa。应力值超过了材料的许用
应力。

在计算过程中，考虑地基沉降，计算了储罐的应力分布情况。根据有关规定[4]，储罐的沉降允许值为350mm，但此沉降为地基的整体沉降值，若整个储罐统一随地基沉降，则不会在储罐上产生额外的应力。计算中考虑的是相对沉降值，即考虑中间回填沙与周围环梁支撑的相对沉降值。本计算中考虑的是环梁固定不动，中间回填沙有相对沉降，分别计算了沉降值为10mm和20mm时的应力分布。计算表明，地基沉降对储罐侧壁的应力分布影响不大，储罐底部的应力分布形式也没有太大的变化，地基沉降的主要后果是底板与周围环板焊接部位最薄处的应力水平更高，此处变形更大。当地基沉降值为10mm时，储罐底板最薄处Tresca应力最大值为879MPa。当地基沉降值为20mm时，储罐底板最薄处Tresca应力最大值为1006MPao

4储罐安全评价
根据前面ABAQUS有限元软件对储罐的计算分析结果，借鉴第三强度理论，根据压力容器分析设计标准[5]对储罐各部分的安全性进行评定。
对于最上层罐壁，使用的材料为Q235-B，许用应力为161MPa，由图5知，最上层罐壁的环向应力小于100MPa，因此对于最上层罐壁，应力小于材料许用应力值，能够满足强度要求。
对干其它各层罐壁，使用的材料为SPV490Q，许用应力为261MPa。由图9知，计算出的罐壁最大应力值为302MPa，因此若按照目前的设计，则储罐是不安全的。但是本计算中考虑储存的介质是水，而储罐未来储存的是原油，其密度小干水根据工程经验估计密度一般为水的80%。按照这个比例，则罐壁最大应力值为2416MPa，则储罐的应力小于许用应力261MPa，因此储罐使用时是安全的。但是在储罐正式使用前，需进行水压试验，此时储存的介质为水，注意到最大应力已经超过许用应力值，因此水压试验时水的高度需要降低，不能完全等同于储存油的液面高度。
对于底板材料，除周围与环板焊接部位外，其它部位应力都低于材料SPV490Q的许用应力为261MPa能够满足强度要求。对于外围最薄处，将具有二次应力性质的成分并入一次薄膜应力，并进行如下的分析。
将罐辟中的应力进行应力分半，分别给出了蒲膜应力，蒲膜应力一变曲应力，总Tresca应力，如图(
所示。从图中看出，对于底板内侧，薄膜应力强度(S)为5.3MPa，薄膜应力+弯曲应力(S)最大值为162MPa峰值应力(Sy)为362MPa。对于底板外侧，薄膜应力强度(S)为53MPa，薄膜应力十弯曲应力(S)最大值为141MPa峰值应力(Sv)为334MPa。对于SPV490Q材料，许用应力[]为261MPac根据JB4732-95规定，液压试验条件下，当评定点满足下式时，材料应力满足强度要求
S1.25Sm Su<1875S
其中S为薄膜应力，S为材料的设计应力强度，即许用应力，Sm为薄膜应力+弯曲应力[56]。
将罐底板最薄处的应力代入上面两式，均能满足，说明此处的应力水平能够满足JB4732-95标准要求。是安全的。

5结论

对双盘式浮顶罐进行有限元分析计算，得到了储罐的应力分布规律，并结合压力容器设计规范，对储罐的应力进行了应力评价。
若考虑储罐的介质为原油，储罐罐壁应力能够满足强度要求，罐壁的最大应力值在第三块厚度为12mm的罐壁上，最大环向应力值为300MPa。除最上和最下段罐壁外，罐壁应力分布均匀，并且均保持一个较高的应力水平。
罐底应力水平比较低，均能够满足强度要求。但是罐底边缘与罐底环板焊接部位很薄，由于罐壁弯矩作用，此处变形很大，并且应力很高。对此处的应力进行分类，并且根据JB4732-95规定对应力进行评价。此处的应力也能够满足要求。
通过对罐底和罐壁应力进行计算和分析评价，该储罐的设计能够满足相关法规的要求，当储罐储存的原油达到设计的最高液位时，储罐是安全的。