Fe-safe Verity焊缝疲劳分析简介

一. Verity焊缝疲劳分析的必要性

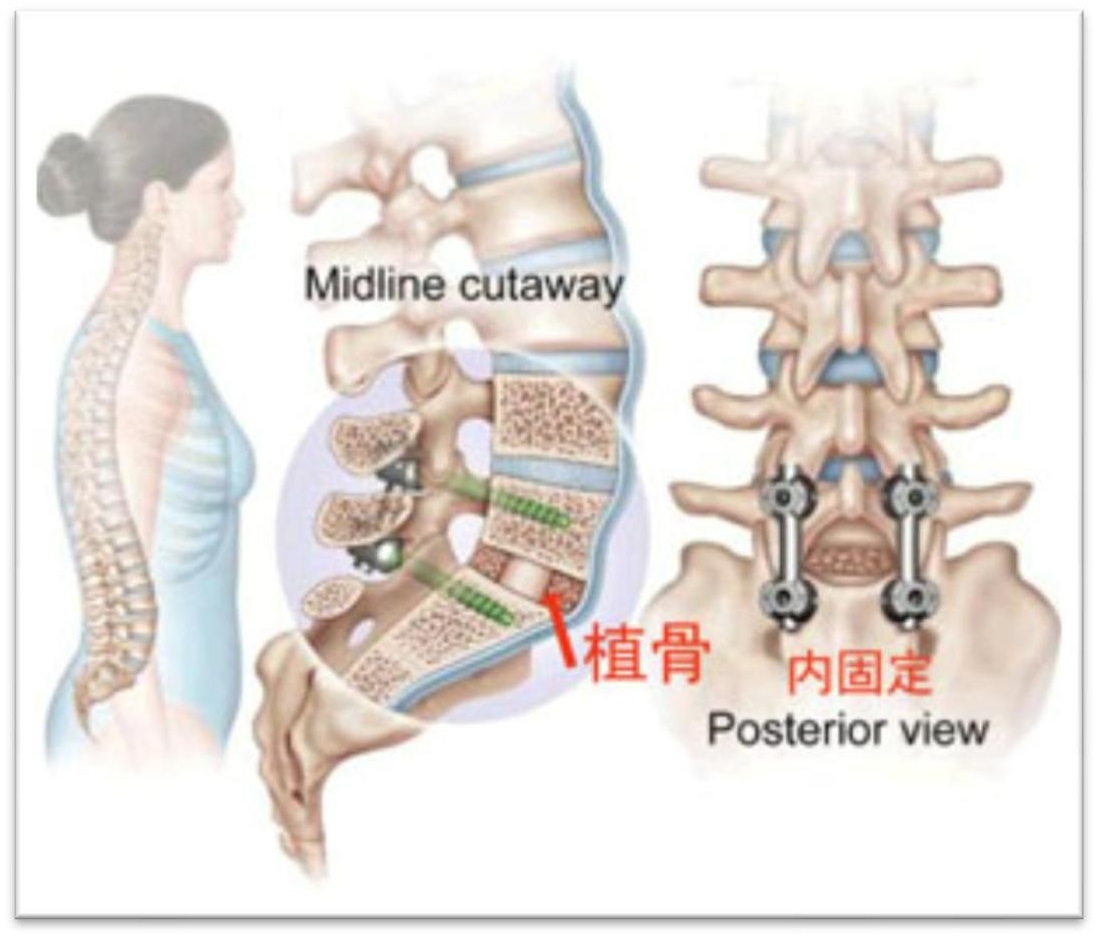
焊接连接是工业领域上非常常见的结构连接方式，在结构设计中具有非常重要的地位，因此焊接的结构强度和疲劳强度都非常重要。一般情况下，平板焊接钢结构焊缝的屈服强度和抗拉强度都不低于其母材，但是焊缝的疲劳强度却远远低于母材的疲劳强度，焊缝失效的主要形式为疲劳，所以焊缝疲劳强度分析十分必要。焊缝的抗疲劳性能很大程度上取决于焊缝的宏观和微观几何形状，影响焊缝疲劳强度得因素很多，比如动态应力，平均应力，焊接残余应力等。

传统的焊接疲劳分析方法是通过有限元分析软件来计算焊缝处的应力，然后根据焊接结构的不同类型定义应力寿命S-N曲线来计算焊缝的疲劳寿命。一般来说，有限元网格的大小直接影响仿真分析的结构应力结果，特别在应力集中位置（焊接位置通常有应力集中），其影响更大，因此传统焊接疲劳分析方法无法准确预测焊缝处的疲劳寿命。

2006年最新版本的Fe-safe引入了一个全新的“Verity”模块，可以很好地解决上述问题。该模块的核心技术来源于美国著名的科技研发公司Battelle的JIP（Joint Industry Project）项目研究成果，该研究成果“Mesh-insensitive Structural Stress Method”是在通用有限元分析程序计算结果基础上，针对板壳、实体等结构连接形式，专门开发计算等效Structural Stress的程序，使得最后的应力计算结果不具有网格敏感性，即在不同网格尺寸下都能获得精确一致的疲劳仿真结果。

二. Verity焊缝分析介绍

Verity的等效结构应力法是一种新型焊接结构疲劳寿命预测技术, 可广泛应用于不同工业领域的各类形式焊接承载部件的焊趾疲劳分析, 如压力容器、管道、海上平台、船舶、地面车辆等结构的管件及平板焊接接头。该方法主要基于以下2项关键技术:

1. 考虑焊趾部位的结构应力集中效应, 应用改进线性化法或节点力法分析其结构应力(即热点应力) , 确保计算结果对有限单元类型、网格形状及尺寸均不敏感, 从而有效区分不同接头类型的焊趾结构应力集中情形。

2. 以结构应力为控制参数计算应力强度因子, 在主要考虑焊趾缺口、结构板厚、载荷模式等因素影响的基础上, 基于断裂力学分析确定与疲劳寿命直接相关的应力参数, 导出等效结构应力转化方程。

3. 将其应用于处理疲劳试验结果数据, 构建出单一通用的疲劳设计主S —N曲线, 从而基于等效结构应力并结合该主S —N 曲线进行焊接结构的疲劳强度评定及寿命预测。

2.1 等效结构应力定义

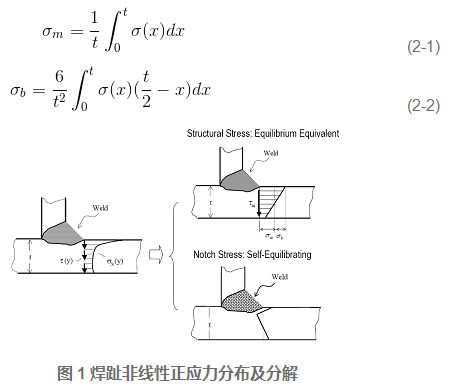
在焊趾缺口附近沿板厚方向的应力分布通常是非线性的, 焊趾部位垂直于竖向假设裂纹面的实际正应力分布如图1 所示。按平衡等效条件, 该实际缺口的正应力可分解为沿板厚 t 分布的膜正应力σm 、弯曲正应力σb 和非线性正应力峰值σp , 结构应力即定义为焊趾表面膜正应力和弯曲正应力之和。若已知板厚t 方向的正应力分布函数σ(x) , 则结构应力σs 可通过常规的线性化法按下式确定：

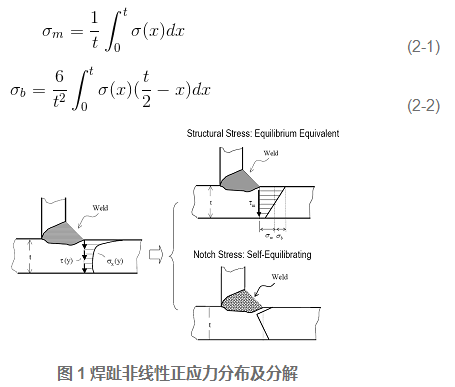
2.2 基于节点力法的等效结构应力计算

节点力法结构应力的计算原理: 组成结构应力的膜正应力分量和弯曲正应力分量分别由作用在其板厚截面上的轴向线力F和线力矩M导致，而轴向线力和线力矩是由有限元方法计算得到的节点力计算得到，如图2所示；其中轴向线力与节点力的平衡方程如下：

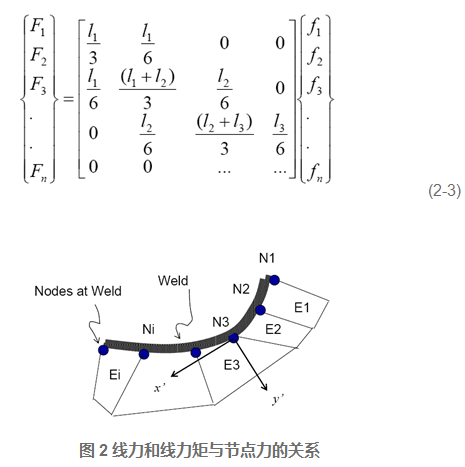
由如上公式计算出焊缝处的线力和线力矩后，通过材料力学的简单梁公式计算膜正应力和弯曲正应力：

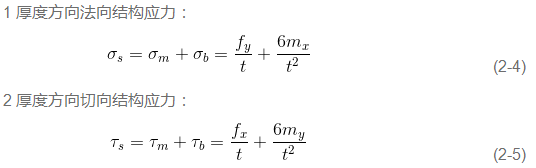
2.3 结构应力的网格不敏感性

为了验证结构应力的计算结果对有限单元类型、网格形状及尺寸均不敏感，本文将从如下几个不同的方面进行对比

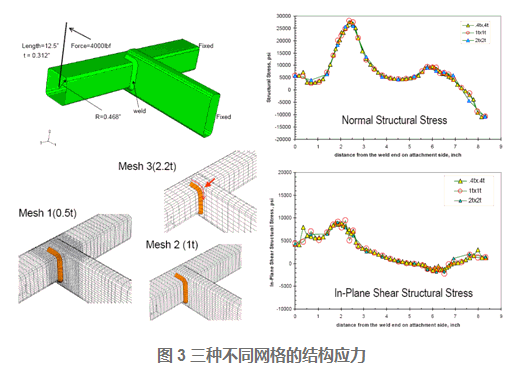
1. 比较不同的单元尺寸：

对于如图3所示的焊接结构模型，不同单元尺寸（分别为0.5t*0.5t，1.0t*1.0t，2.0t*2.0t）的有限元结果转化的结构应力（Structural Stress）结果沿焊缝线基本一致，这说明结构应力（Structural Stress）对于有限元模型的单元尺寸不敏感。

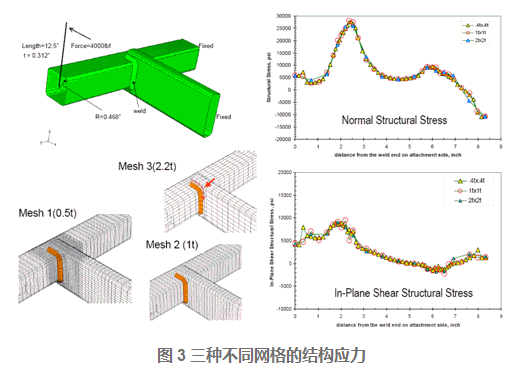
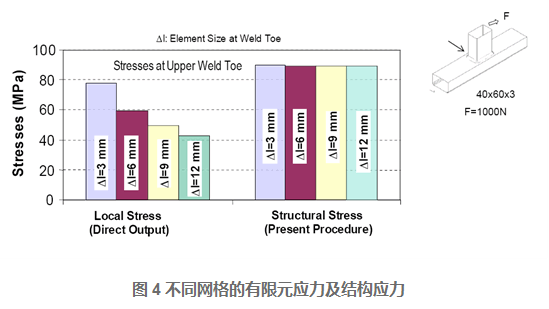
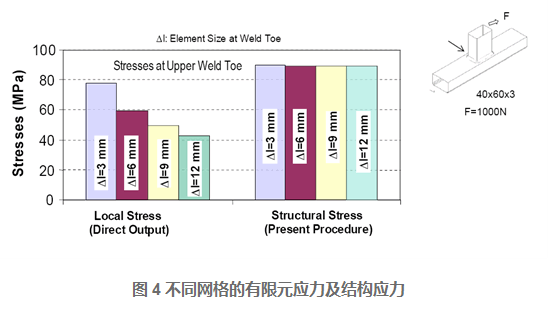
对于如图4所示的焊接结构模型，不同单元尺寸的有限元模型计算得到的应力及转化的结构应力（Structural Stress）结果如下图所示，这说明焊趾处的应力随网格尺寸变化很敏感，而结构应力（Structural Stress）对于有限元模型的单元尺寸不敏感。

2. 比较不同的单元类型和单元尺寸：

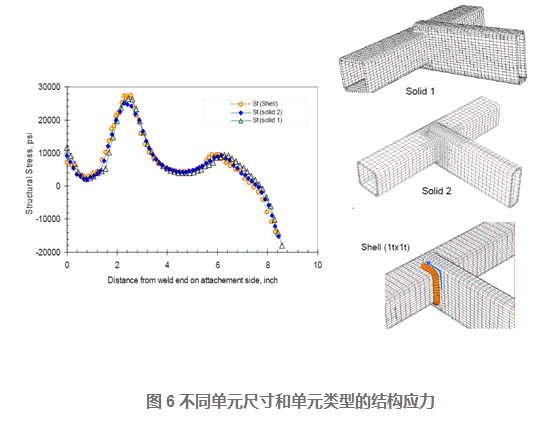
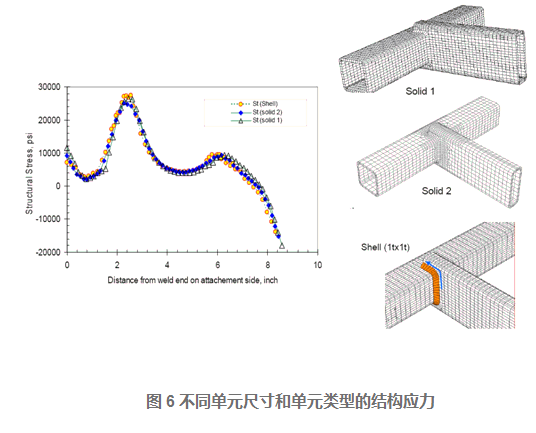
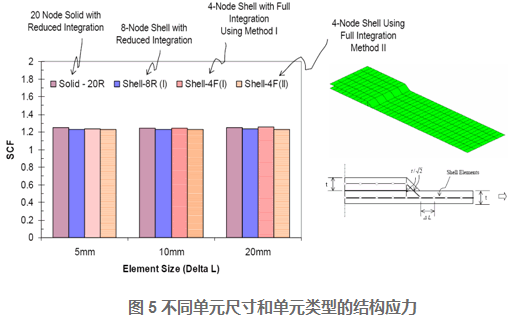
对于如图5所示的焊接结构模型，不同单元尺寸和不同单元类型的有限元模型应力转化的结构应力（Structural Stress）结果如下图所示，这说明结构应力（Structural Stress）对于有限元模型的单元尺寸和单元类型不敏感。

对于如图6所示的焊接结构模型，不同单元尺寸的实体单元和壳单元的有限元模型应力转化的结构应力（Structural Stress）结果如下图所示，这说明结构应力（Structural Stress）对于有限元模型的单元尺寸和单元类型不敏感。