血管支架的压握( crimping)和释放( expansion)过程及其疲劳分析
血管支架的压握( crimping)和释放( expansion)过程及其疲劳分析是支架设计和性能评估的关键环节,涉及复杂的力学行为和生物医学工程问题。以下是有限元分析( FEA)在此领域的应用要点和流程:
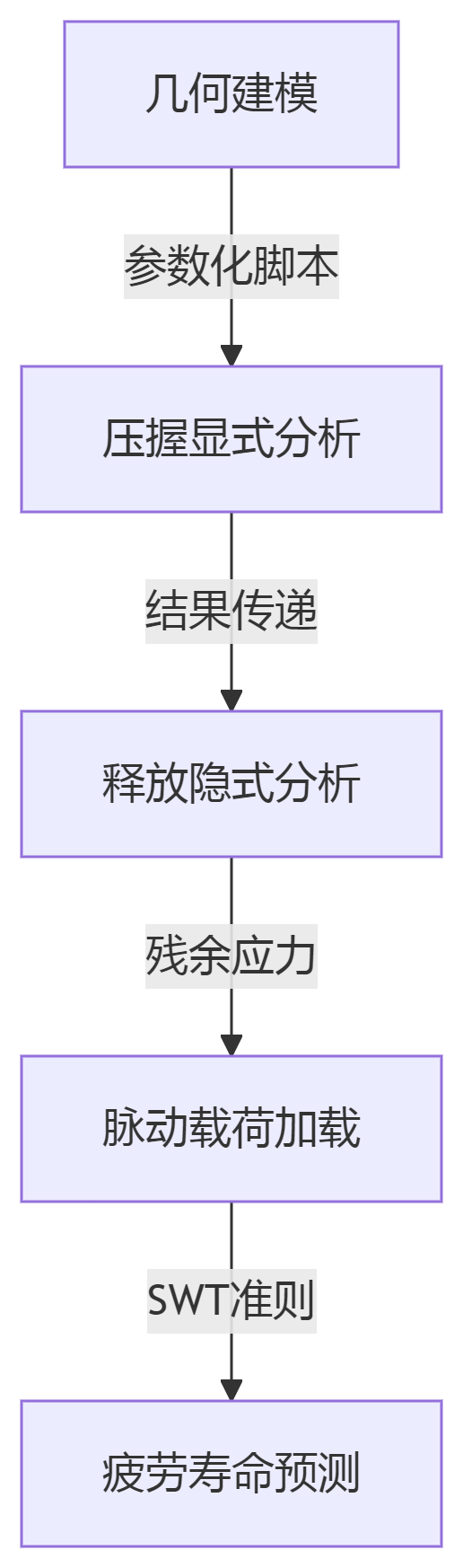
1. 压握与释放过程模拟
1.1 几何与材料模型
-
几何模型:基于支架设计(如开环、闭环结构)建立参数化三维模型,需考虑支架丝厚度、连接点等细节。
-
材料模型:
-
超弹性材料(如镍钛合金 Nitinol):使用 Auricchio 或 Shape Memory Alloy 本构模型。
-
塑性材料(如不锈钢、钴铬合金):定义塑性硬化准则(如各向同性/随动硬化)。
-
聚合物支架:考虑粘弹性或超弹性行为。
-
1.2 边界条件与载荷
-
压握过程:模拟支架被球囊或机械装置径向压缩至输送导管内(直径减少 50%~90%),需定义接触(支架-压握工具)和摩擦(μ≈0.1~0.2)。
-
释放过程:
-
自扩张支架:通过撤除外约束模拟弹性恢复,需考虑血管壁的约束。
-
球囊扩张支架:施加径向位移载荷模拟球囊膨胀。
-

1.3 关键输出
-
应力/应变分布(重点关注高应力区域如连接点)。
-
塑性变形(永久变形量)。
-
回弹率(释放后的直径恢复率)。
2. 疲劳分析
支架在体内承受周期性载荷(如心跳导致的血管脉动),需评估其抗疲劳性能(通常要求 10 年寿命,约 4×10⁸ 循环)。
2.1 疲劳载荷条件
-
脉动压力:典型幅值 80~120 mmHg(约 10~16 kPa),频率 1~2 Hz。
-
多轴载荷:可能叠加弯曲、扭转(如冠状动脉支架)。
2.2 疲劳分析方法
-
应力-寿命(S-N)法:
-
适用于高周疲劳,需材料 S-N 曲线(实验获取)。
-
修正因素:表面粗糙度、尺寸效应、平均应力(Goodman/Gerber 修正)。
-
-
应变-寿命(ε-N)法:
-
适用于局部塑性变形(如 Nitinol 支架)。
-
使用 Coffin-Manson 方程:Δε/2 = σ_f'/E (2N)^b + ε_f' (2N)^c。
-
-
损伤累积理论(如 Miner’s Rule)。
2.3 有限元实现
-
准静态分析:先模拟压握-释放过程,获取残余应力场。
-
周期性载荷分析:
-
施加脉动压力载荷(幅值 ΔP)。
-
提取关键节点的应力/应变幅值(Δσ/Δε)。
-
-
疲劳寿命预测:
-
结合材料疲劳参数(如 Nitinol 的 ε_f'≈0.1~0.3)计算寿命。
-
安全因子评估(通常要求 N≥10⁸ 循环)。
-
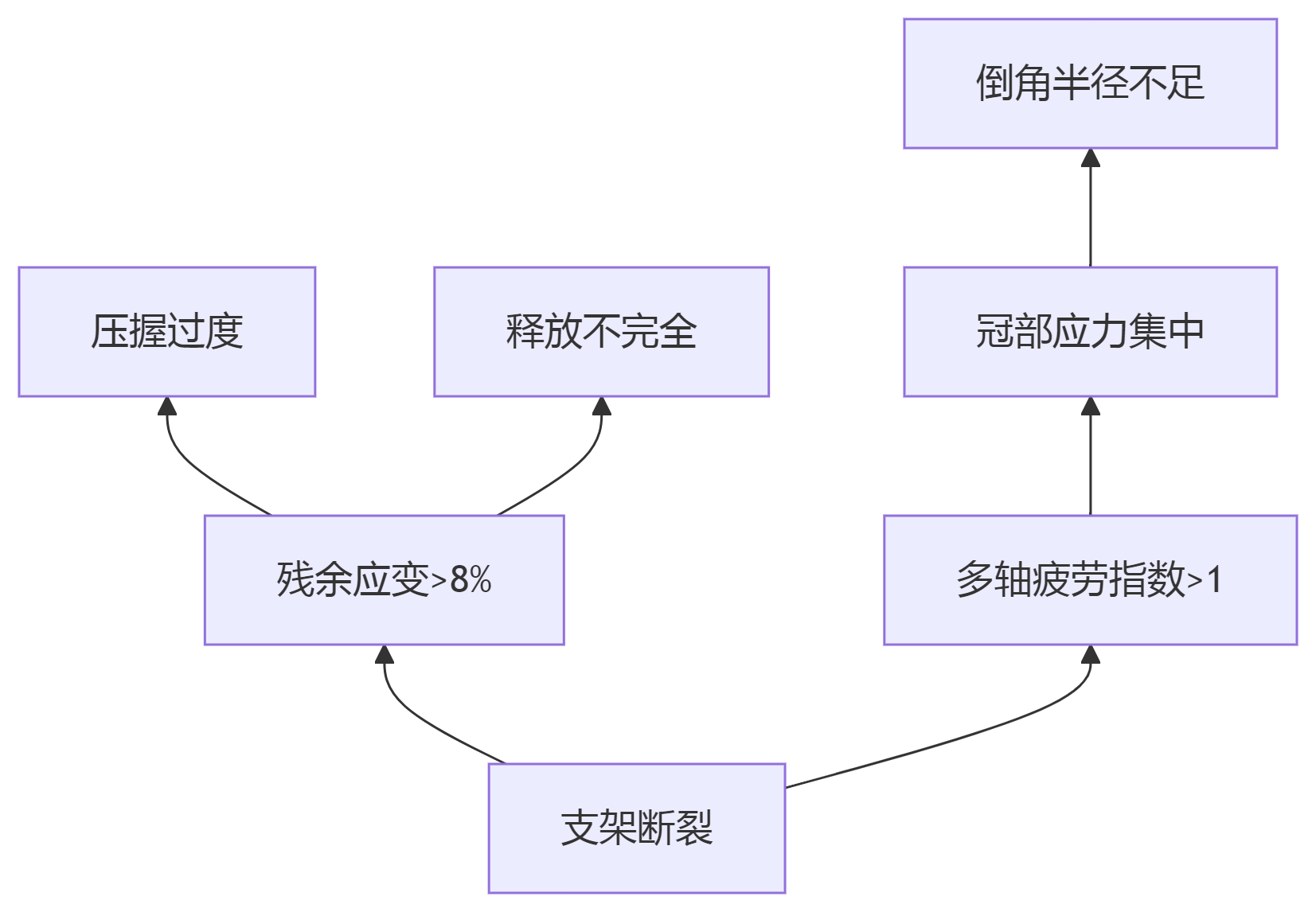
-
3. 关键挑战与解决方案
-
材料非线性:使用增量迭代法(如 Newton-Raphson)处理大变形。
-
接触收敛问题:调整罚函数参数或使用对称接触算法。
-
计算效率:采用子模型技术(Submodeling)聚焦高应力区域。
-
实验验证:通过加速疲劳试验(如 50 Hz 测试)对比 FEA 结果。
4. 常用软件
-
ABAQUS:适用于超弹性/塑性材料和非线性接触。
-
ANSYS:提供 Fatigue Tool 模块。
-
COMSOL:多物理场耦合分析(如血流-支架相互作用)。
-
LS-DYNA:显式动力学分析(适用于快速压握过程)。
5. 相关标准与文献
-
ISO 25539-2:心血管植入物-血管支架的标准。
-
ASTM F2477:血管支架疲劳测试指南。
-
文献参考:
-
Auricchio et al. (2016) 对 Nitinol 支架的本构模型研究。
-
Wei et al. (2020) 关于多轴疲劳的有限元方法。
-
通过有限元分析,可优化支架设计(如减少应力集中)、预测疲劳寿命,并降低临床试验风险。需注意模型假设(如忽略血流剪切力)与实验数据的校准。
- 上一篇:PCB板主要元器件焊点热应力疲劳分析的-仿真缺陷 2025/7/4
- 下一篇:血管支架压握释放有限元疲劳分析 2025/7/4
